5. sada domácich zadaní
Najneskorší termín odovzdania: 31.10.2021 (nedeľa) o 18:00
Odovzdávané súbory: KorytnaciSvet.java
Doplňujúce požiadavky:
- riešenia, ktoré nebude možné skompilovať (t.j. riešenia so syntaktickými chybami) nebudú hodnotené,
- zdrojový kód správne naformátujte (CTRL+SHIFT+F),
- očakáva sa vhodne okomentovaný zdrojový kód
Korytnačí svet
Uvažujme triedu KorytnaciSvet, ktorá rozširuje triedu WinPane:
import sk.upjs.jpaz2.*;
public class KorytnaciSvet extends WinPane {
/**
* Referencia na pole korytnaciek
*/
private Turtle[] korytnacky = null;
/**
* Inicializacna metoda (konstruktor)
*/
public KorytnaciSvet() {
this.korytnacky = new Turtle[0];
}
/**
* Metoda na pridanie korytnacky na zadanych suradniciach
*/
public void pridajKorytnacku(int x, int y) {
Turtle novaKorytnacka = new Turtle();
this.add(novaKorytnacka);
novaKorytnacka.setPosition(x, y);
Turtle[] noveKorytnacky = new Turtle[this.korytnacky.length + 1];
System.arraycopy(this.korytnacky, 0, noveKorytnacky, 0, this.korytnacky.length);
noveKorytnacky[noveKorytnacky.length-1] = novaKorytnacka;
this.korytnacky = noveKorytnacky;
}
@Override
protected void onMouseClicked(int x, int y, MouseEvent detail) {
if (!(detail.isAltDown() || detail.isControlDown() || detail.isShiftDown())) {
this.pridajKorytnacku(x, y);
}
}
}
Dôležité: Existujúce metódy a konštruktor nemodifikujte. Rovnako nepridávajte vlastné inštančné premenné.
Výstrel na ťažisko (2 body)
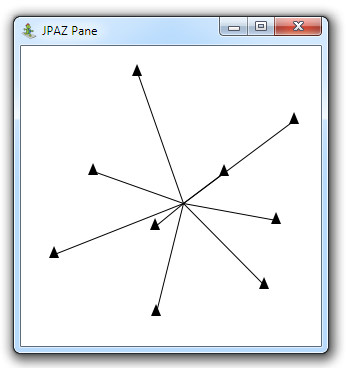
Do triedy KorytnaciSvet pridajte metódu vystrelNaTazisko, ktorej výsledkom bude to, že každá korytnačka nakreslí čiaru zo svojej pozície do ťažiska všetkých korytnačiek. Súradnice ťažiska korytnačiek možno vypočítať ako priemer pozícii jednotlivých korytnačiek (napr. x-ová súradnica ťažiska je priemerom x-ových súradníc korytnačiek): http://en.wikipedia.org/wiki/Centroid#Of_a_finite_set_of_points
Bombastické korytnačky (2 body)
Keďže korytnačky v JPAZe sú nezničiteľné, ministerstvo obrany za rozhodlo využiť korytnačky v kresliacej ploche na testovanie účinkov explózií. Do kresliacej plochy umiestnili nálož so zadanou silou (parameter sila) na pozíciu [x, y]. Pri explózii nálože vznikne tlaková vlna, ktorá odhodí korytnačky v smere od miesta explózie. Ak uvážime zjednodušený fyzikálny model, korytnačka vzdialená d od miesta explózie so silou S je odhodená o vzdialenosť S2/d4. Budeme predpokladať, že žiadna korytnačka sa nenachádza v mieste explózie. Do triedy KorytnaciSvet pridajte metódu explozia, ktorá odsimuluje účinky explózie nálože so zadanou silou a umiestnenej na zadanej pozícii. T.j. všetky korytnačky v ploche sa presunú (bez kreslenia trajektórie pohybu) na miesto, kam ich odhodí tlaková vlna, a budú nasmerované v smere od miesta explózie. Metóda vráti najväčšiu vzdialenosť, o akú bola odhodená nejaká z korytnačiek v ploche.
Najrýchlejšia korytnačka (2 body)
Korytnačka sa dokáže otáčať rýchlosťou 1° za sekundu. Rýchlosť pohybu korytnačky je jednotková vzdialenosť („1 pixel“) za sekundu. Korytnačka sa nedokáže v jednom okamihu súčasne posúvať aj otáčať. Zároveň, aby stále videla na cestu, korytnačka sa pohybuje len smerom vpred (t.j. necúva). Nech C je bod na súradniciach [x,y]. Za aký najkratší čas v sekundách sa do bodu C môže dostať prvá korytnačka? Nezabudnite, že korytnačka sa môže otáčať v smere aj proti smeru hodinových ručičiek.
Do triedy KorytnaciSvet pridajte metódu casDoPrichodu. Metóda casDoPrichodu má 2 parametre x, y - súradnice bodu C, a vráti najmenší čas v sekundách, za aký sa niektorá z korytnačiek vie dostať do bodu C.
Rada (matematika ZŠ): Vonkajší uhol k uhlu α má veľkosť 360°-α.
Rada: Ak chcete používať metódu s ktorou ste doposiaľ nepracovali prečítajte si k nej dokumentáciu.
Vzdialenostný histogram (3 body)
Nech d je nenulové kladné číslo (d>0) a C je bod na súradniciach [x,y]. Na základe vzdialenosti od bodu C môžeme korytnačky rozdeliť do „zón“. Povieme, že korytnačka sa nachádza v i-tej zóne okolo bodu C, keď jej vzdialenosť od bodu C je v intervale ⟨i⋅d, i⋅d+d). Do triedy KorytnaciSvet pridajte metódu histogram, ktorá vráti referenciu na pole, v ktorom na indexe i bude uložený počet korytnačiek nachádzajúcich sa v i-tej zóne okolo zadaného bodu C. Dĺžka vráteného poľa nech je najmenšia možná s tou vlastnosťou, že súčet prvkov poľa bude rovný počtu korytnačiek v ploche. Metóda histogram má 3 parametre: x, y - súradnice bodu C a šírku zón d.
Rada: Odporúčame si najprv vypočítať maximálnu vzdialenosť medzi bodom C a ľubovoľnou korytnačkou v ploche. Na základe tohto vypočítate, aké veľké pole potrebujete vrátiť.
Do štvorca (3 body)
Do triedy KorytnaciSvet pridajte metódu doStvorca, ktorá pravidelne umiestni korytnačky v kresliacej ploche na strany štvorca so stredom v strede kresliacej plochy a so zadanou dĺžkou strany. Môžete predpokladať, že počet korytnačiek v ploche je deliteľný číslom 4. Do rohov štvorca korytnačky neumiestňujeme.

Prestrelka (5 bodov)
A je to tu. Zločin zavítal aj do korytnačieho sveta. Máme tu prvú prestrelku. Vo svete korytnačiek však aj prestrelky majú svoje pravidlá:
- ako prvá začína strieľať zvolená korytnačka (určená indexom - indexy korytnačiek rastú od 0 v poradí pridania korytnačiek do korytnačieho sveta),
- strieľajúca korytnačka strieľa vždy na najbližšiu doposiaľ nezasiahnutú korytnačku (výstrel znázorňujeme tak, že strieľajúca korytnačka sa natočím smerom k cieľu a dráha strely je vyznačená čiarou od strelca k cieľu),
- každá korytnačka strieľa na cieľ ihneď po svojom zasiahnutí.
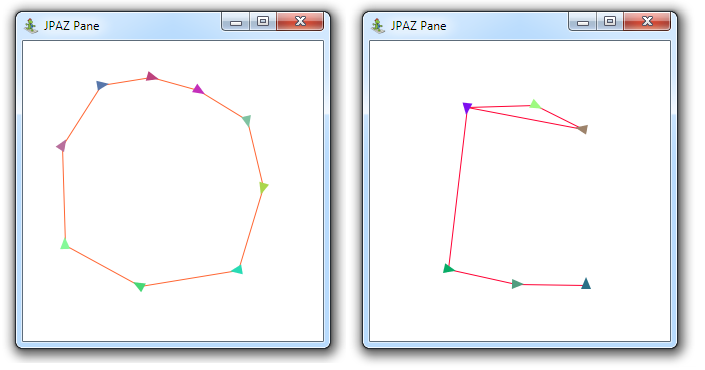
Do triedy KorytnaciSvet pridajte metódu prestrelka, ktorá zadanou farbou znázorní strely vypálené pri prestrelke, ktorú začne korytnačka s indexom určeným parametrom metódy.
Rada: Na uloženie toho, ktorá korytnačka už bola zasiahnutá, môžete využiť lokálne referencované pole.
Poznámky
Vzdialenostný histogram
Keďže ObjectInspector nezobrazuje metódy s parametrom alebo návratovou hodnotou typu referencia na pole, pri riešení úlohy si odporúčame vytvoriť pomocnú metódu:
int[] p = this.histogram(x, y, d);
System.out.print("histogram(" + x + ", " + y + ", " + d + "): ");
System.out.println(Arrays.toString(p));
}
